Ondas

Introdução

Apesar de estar presente em nosso quotidiano, o fenômeno ondulatório é de difícil compreensão, pois, apesar de haver movimento de partículas (ou de fótons), essas partículas não são transportadas através do espaço junto com a onda. As partículas na onda oscilam em torno de um ponto de equilíbrio, na própria direção de propagação da onda transversal, ou na direção perpendicular à direção de propagação da onda. Uma combinação dessas duas oscilações pode resultar em movimento circular de partículas em uma onda na superfície da água, por exemplo.

E Então, o que as ondas transportam se não matéria? O que são ondas, afinal?

Em geral, as ondas necessitam de um meio de propagação. Estas ondas são classificadas como ondas mecânicas. As ondas eletromagnéticas, que serão estudadas separadamente, não necessitam de um meio de propagação; propagam tanto no vácuo como no ar, na água e em outros materiais.

Atividade 1: Liste alguns exemplos de ondas que você conhece.

Voltemos às ondas mecânicas, assunto desta disciplina. Entender um pouco dos conceitos de ondas mecânicas será muito útil para o entendimento das ondas eletromagnéticos e outros fenômenos físicos oscilatórios.

Definindo onda. Em Física, podemos definir onda como uma perturbação ou oscilação que se propaga no espaço (ou espaço-tempo) acompanhado de transferência de energia (e não de matéria).

Atividade 2: Pesquise outras definições de onda.

As ondas consistem de oscilações ou vibrações em torno de pontos (quase) fixos, em equilíbrio. As ondas são descritas por equações de ondas que mostram como a perturbação evolui no tempo. Naturalmente, a equação de onda depende do tipo de onda. Muitas ondas são do tipo senoidal e a equação de onda é descrita por uma equação senoidal. Estudaremos aqui as ondas senoidais. A combinação ou interferência de ondas senoidais resultam em diferentes tipos de ondas periódicas.

Vídeo-aula: Propriedades das ondas

Vídeo-aula: Ondulatória

Atividade 3: Compare estes dois vídeo lavando levando em cona aspectos pedagógicos, tais como qualidade do vídeo, conteúdo, clareza e potencial para ensino e aprendizagem de Física, e outros aspectos que você desejar.

Opcional: Teste seu inglês! Assista a este vídeo em inglês sobre ondas.

Simulação 1: Onda na corda

Onda na corda é um exemplo de onda transversal em uma dimensão. crie um pulso ou um trem de ondas e determine as suas propriedades. Observe também as ondas refletidas quando a extremidade da corda está fixa ou livre.

Simulação 2: Ondas na superfície

(Clique sobre a figura para abrir a simulação em uma janela. Requer o aplicativo Java instalado em seu computador -grátis.)

Click to Run

Simulação 3: Carga radiante

Ondas transversais e ondas longitudinais
Em geral, as ondas são transversais ou longitudinais. Nas ondas longitudinais, as partículas do meio oscilam na direção perpendicular à direção de propagação da onda.
Nas ondas longitudinais, as partículas do meio oscilam na mesma direção de propagação da onda, como ilustra a animação abaixo de um pulso de onda  se propagando através de uma mola comprida.

Note que em ambos os casos, as partículas do meio não se propagam junto com a onda; elas oscilam em torno da posição de equilíbrio.

Vídeo: Ondas longitudinais e ondas transversais

De acordo com este vídeo, Uma onda longitudinal, ou de onda de compressão, é criada por uma perturbação ao long da direção de propagação da onda. Uma onda transversal é criada por uma perturbação perpendicular à direção de propagação da onda.

Vídeo: Ondas longitudinais

.

Propriedades da onda
Veja no vídeo abaixo, algumas propriedades das ondas.

Vídeo: Propriedades de Ondas

Após assistir ao vídeo, liste algumas propriedades de ondas.

Funções de onda

Vimos que as ondas podem adquirir formas variadas. Alguns tipos de ondas são as ondas senoidais. quadradas, triangulares e tipo dente de serra. As equações matemáticas que descrevem essas ondas são relativamente simples. Aqui, estudaremos as ondas senoidais, que você já deve estar familiarizado quando estudou o movimento oscilatório e o movimento harmônico simples (MHS).

Em geral, o sistema que causa a perturbação que gera onda senoidais realiza um MHS, que é descrito por uma função senoidal. Você já deve ter estudado o MHS senão, recomendamos que faça uma revisão sobre esse tópico. Clique aqui para acessar uma simulação sobre o MHS.
No MHS, como a equação de onda senoidal é descrita por uma função seno (ou cosseno) do tipo y(x,t) = Acos(kx - wt). Esta equação descreve uma onda se propagando para a direita, com as seguintes características: amplitude A, número de ondas (ou frequência espacial ou constante de propagação) k = 2p/l e frequência angular w = 2pf = 2p/T, onde l é o comprimento de onda, f é a frequência e T é o período (T = 1/f).
Na figura abaixo vemos um sinal elétrico (voltagem x tempo) senoidal, que representa, por exemplo, a voltagem elétrica de nossa casa, onde a frequência f = 60 Hr, e Vrme = 0,7 x Vp. Como dissemos, o fenômeno ondulatório está presente em toda parte!
Discuta com seus colegas o fenômeno ondulatório na corrente alternada (lembre-se: V = R x I, Lei de Ohm, onde V é a voltagem, R é a resistência e I é a corrente elétrica). Como seria o gráfico da corrente elétrica? A corrente e a voltagem estão em fase?

Onda elétrica alternada

A seguir, vamos demonstrar que a função de onda, para uma onda senoidal, é dada por y(x,t) = Acos(kx + wt) ou y(x,t) = Acos(kx - wt), se a onda se propagar, respectivamente para a direita ou para a esquerda.
A demonstração é semelhante à mostrada na sala de aula.
Vamos considerar uma onda se propagando para a direita e, de modo semelhante, demonstramos o outro caso. Imaginemos, por exemplo, uma onda transversal em uma corda.
Na origem da coordenada, em um instante t, um ponto da da onda (corda), oscila sonoialmente de acordo com a equação y(x = 0, t) = y(t) = Acoswt. Em um instante posterior, t' = t + x/v, esta onda com velocidade v se propagou para a direita, de uma distância x, e a equação da onda se torna y(x,t) = Acos(t - x/v) = Acos(x/v - t). Sabemos que a velocidade da onda v = fl e que w = 2pf. Substituindo na última equação, obtemos y(x,t) = Acos(kx - wt), onde k = 2p/l é o número de ondas. Verifique todas as passagens!

Velocidade de onda
Se a uma onda se propagando para a direita no eixo-x é descrita pela função de onda y(x,t) = Acos(kx + wt), a velocidade a onda (na direção x) é dada pela derivada dx/dt (não confundir com a velocidade dy/dt de uma partícula na onda). Podemos verificar que v = w/k (verifique as unidades!). Na equação da onda, o argumento é a fase f da onda, ou seja, f = kx - wt.
Se f é constante, derivando esta equação com relação ao tempo (df/dt = 0 e dx/dt = v), vemos que v = w/k (verifique!).
Por essa razão, a velocidade da onda também é denominada velocidade de fase da onda.
Assim, uma definição formal de velocidade da onda é: a velocidade que nos deslocamos ao lado da onda de modo que a fase, f = kx - wt, de um dado ponto da onda seja constante.
Temos, portanto, que uma onda sonidal se propagando com velocidade constante v, a fase f é constante e igual a kx - wt.

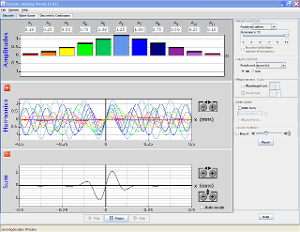
Série de Fourier
Além da importância anatural das ondas senoidais, descritas por uma função do tipo y(x,t) = Asen(kx - wt), que descreve uma onda senoidal de amplitude A, frequência angular w e número de onda k, podemos obter infinitas ondas periódicas somando ondas senoidais, como mostra a simulação abaixo.

Interferência de ondas
Duas ou mais ondas interferem construtiva ou destrutivamente. Veja a simulação abaixo.

Applet: interência de duas ondas harmônicas (senoidais). Clique aqui (requer Java instalado).

Exercício interativo: Interferência de ondas.


Simulação: Fourier - Fazendo Ondas

Click to Run

Velocidade de fase e velocidade de grupo (opcional)
A superposição de duas ou várias ondas pode resultar em um envelope de ondas. A velocidade da "onda envelope" (curva verde na figura abaixo) é denominada velocidade de grupo, e a velocidade da onda contida no envelope (curva azul) é a velocidade de fase.

Velocidade de fase e velocidade de grupo

Applet: velocidade de grupo e de fase. Clique aqui.
Applet: demonstração da velocidade de grupo. Clique aqui.

Onda com velocidade de grupo e de fase em direções opostas.

Ondas Estacionárias
Como o próprio nome sugere, ondas estacionárias são ondas que não se propagam. Em um meio de propagação de dimensão finita, a onda pode se propagar em uma extremidade do meio e refletor na outra, criando, assim, modos de vibração, ou ondas estacionárias.
Assista aos dois vídeos abaixo sobre ondas estacionárias.

Vídeo-aula: Ondas Estacionárias 1

Vídeo-aula: Ondas Estacionárias 2

Outro vídeo de ondas estacionárias de ondas sonoras. Clique aqui. Em inglês, Standing Waves. Ondas estacionárias na corda da guitarra. Outros applets: Som harmônico, ondas estacionárias como onda de ar (ou líquido) em um tubo.

Applet: Ondas estacionárias; Onda estacionária em uma corda; Instrumento de corda;

Ondas com obstáculo
Veremos agora o que acontece com uma onda ao encontrar um obstáculo. O que acontece depende, na verdade das dimensões do obstáculo. Vamos considerar algumas alternativas.
Aguarde!

Equação de onda

A equação que descreve o movimento de uma onda que se propaga na direção x com velocidade v é: d²y/dt² = v²d²y/dx². Cuja solução geral é y(x,t) = f(vt - x) + g(vt + x).
É fácil verificar que a nossa função de onda senoidal, y(x,t) = Acos(kx - wt), conforme definida acima, é solução da equação acima. verifique!

Energia transportada por uma onda

Definimos onda mecânica como sendo uma perturbação em um meio elástico que transporta energia (e não matéria). Como isso acontece? Onde fica armazenada a energia transportada pela onda?

Antes, vamos recordar o conceito de energia. Energia é a habilidade de realizar trabalho, e trabalho consiste no movimento de um objeto sob a ação de uma força. Numa onda, o que se move? E como se move? A onda se move, porém, o que causa esse movimento é a oscilação da matéria no meio de propagação da onda. Logo, o movimento (oscilatório) da matéria causa o armazenamento e o transporte de energia na onda. Partículas, moléculas, elétrons, são exemplos de pequenas matérias que oscilam, com velocidades incrivelmente elevadas, contra a ação de uma força (restauradora). Cada partícula realiza trabalho sobre outra partícula (vizinha), que também se move e também realiza trabalho sobre outra partícula, e assim por diante.

A energia armazenada é igual à quantidade de trabalho realizado por essas partículas. Desse modo, onda pode também ser definida como sendo a transferência de energia armazenada pelo movimento oscilatório de partículas que realizam trabalho em outras partículas.

Para entender esse fenômeno, vamos analisar o caso de uma onda (transversal) em uma corda sob tensão. A corda, com densidade linear de massa m = m/L, está inicialmente esticada na horizonta, por uma força de tensão F. Quando a corda vibra com amplitude A e frequênca f, uma onda do tipo y(x,t) = Acos(kx – wt) se propaga na direção x.

A potência (P = F.v) da onda na corda é: P = -F_yv_y, onde v_y é a velocidade das partículas da corda, e F_y é a componente vertical da tensão no ponto da corda. F_y = Ftgq = Fdy/dx e v_y = dy/dt (q é o ângulo de desvio do eixo-x da direção da tensão).

Combinando essas equações (veremos isso na sala de aula!), obtemos a potência da onda

P = mw²A²v sen²(kx – wt)

Note que a potência é sempre positiva e oscila. A potência média é igual à metade da amplitude, ou seja,

<P> = P/2 = mw²A²v/2

Observe que a potência depende da densidade da corda, da frequência e da amplitude da onda. Lembrando que a potência é igual à taxa de variação da energia, e que a densidade linear de energia, u = U/L = U/vDt, obtemos (verifique!)

u = P/v = mw²A²sen²(kx – wt)

Derivamos, dessa forma, a potência e a densidade de energia de uma onda se propagando com velocidade v = w/k = (T/m)^1/2.

Apesar da energia ter sido aqui derivada para uma onda na corda, ela pode ser generalizada para qualquer tipo de onda senoidal.

Exercício: qual potência de uma onda se propagando, com frequência f = 1,0 H e amplitude A = 5,0 cm, em uma corda, com densidade m = 150 g/m, esticada horizontalmente por uma tensão F = 95 N?

Links:

Texto com áudio em inglês: Overview of Wave Motion
Texto em inglês. The Physics Classroom: Waves
Mais vídeos de Física: Khan Academy - Física
Vídeo: Ondulatória
Calculadora: Escala Richter
Java: Muitas simulações requerem o aplicativo Java instalado em seu computador. Clique aqui para instalar. É livre!
Signals: Sinais elétricos. Clique aqui.
Applets de Física Geral. Clique aqui.
Eric Weisstein's World of Physics: Wave Motion
Velocidade da onda: Group velocity and phase velocity
Applets: general Physics Applets
Mais applets: Fawler's Physics applets
Theory: Phase and Group Velocity
Álbum de Applets: Album of animations: oscilations, waves and phasors
More applets: General Physics Applets